Dijkstra's Algorithm
- Trace Dijkstra's algorithm (shortest path in weighted graphs) by specifying the values in auxiliary data structures.
E. W. Dijkstra (1930-2002), the legendary Dutch Computer Scientist (and Turing Award winner), discovered an algorithm for finding the shortest path (in weighted graphs).

Dijkstra's algorithm works by exploring the (unexplored) neighbors of the next vertex with the smallest distance to the source vertex. For this reason, the algorithm is also called Shortest Path First (SPF) algorithm.
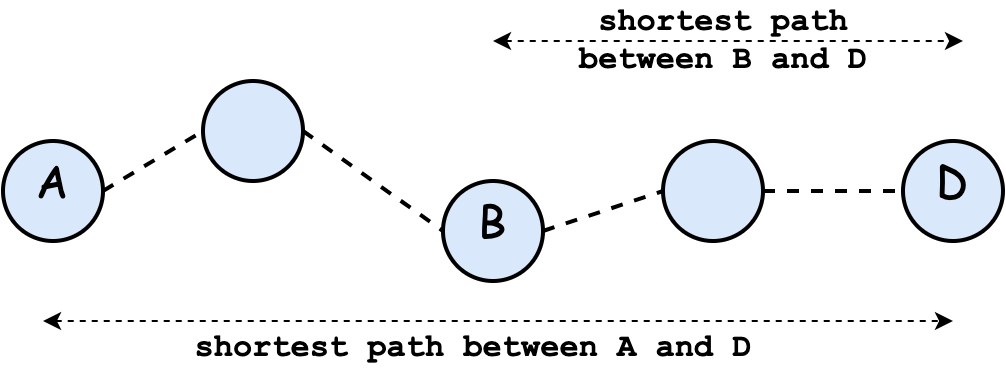
The intuition behind Dijkstra's algorithm is that if vertex $B$ is on the shortest path from $A$ to $D$, then the subpath from $B$ to $D$ is also the shortest path between vertices $B$ and $D$.
For a rigorous analysis and formal proof of correctness, refer to CLRS, Third Edition, Chapter 24, Section 3, Dijkstra's Algorithm on page 658.
Here we will use a demo to understand the steps involved in Dijkstra's Algorithm.
Demo
Exercise Complete the pseudocode for Dijkstra's Algorithm:
for each vertex v
distance[v] = Infinity
previous[v] = null
explored[v] = false
distance[s] = 0 // s is the source
repeat N times
let v be unexplored vertex with smallest distance
________________
for every u: unexplored neighbor(v)
d = distance[v] + weight[v,u]
if ________________
_______________
_______________
Solution
for each vertex v
distance[v] = Infinity
previous[v] = null
explored[v] = false
distance[s] = 0 // s is the source
repeat N times
let v be unexplored vertex with smallest distance
explored[v] = true
for every u: unexplored neighbor(v)
d = distance[v] + weight[v,u]
if d < distance[u]
distance[u] = d
previous[u] = v
Resources
- Wikipedia's entry Dijkstra's algorithm.
- Brilliant's Wiki on Dijkstra's Shortest Path Algorithm.
- Programiz Tutorial on Dijkstra's Algorithm.
- Dijkstra's Shortest Path Algorithm - A Detailed and Visual Introduction on FreeCodeCamp.
- Computerphile YouTube Video on Dijkstra's Algorithm - highly recommended!