Primary Clustering

The problem with linear probing is that it tends to form clusters of keys in the table, resulting in longer search chains.

The reason is that an existing cluster will act as a "net" and catch many of the new keys, which will be appended to the chain and exacerbate the problem.

Exercise Under the assumption of uniform hashing, what is the likelihood that the next key will end up in each "open" position, in the following situation:

Solution

We have ten slots. Assuming uniform hashing, if the table was empty, there is an equal likelihood the next element will be mapped to each index. That is, each position has a $10\%$ chance to home the next element to be inserted.

Given indices $2$, $3$, and $4$ are occupied, if an element is mapped to any of these, it will end up in position $5$. So the chances $2$, $3$ and $4$ will home the next element is $0$. On the other hand, position $5$ has a net chance of $40\%$ to get the next element.

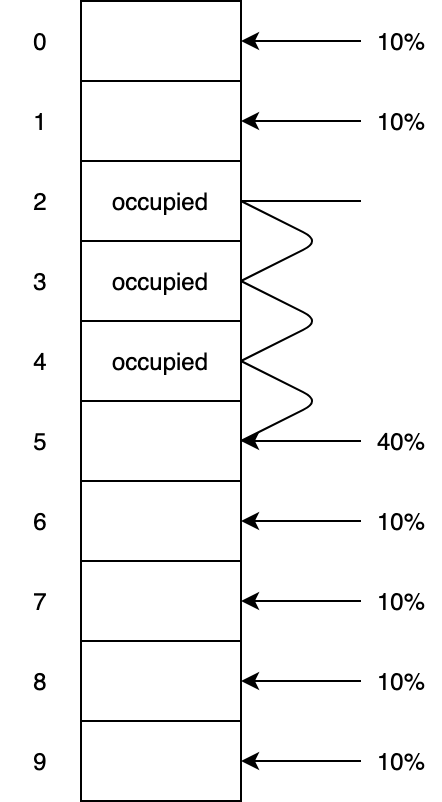
This simple illustration shows how a cluster of elements acts as a net to catch the next element to be inserted.

Each new collision expands the cluster by one element, thereby increasing the length of the search chain for each element in that cluster. In other words, long chains get longer and longer, which is bad for performance since the number of positions scanned during insert/search increases. This phenomenon is called primary clustering (or simply, clustering) issue.

Other probing strategies exist to mitigate the undesired clustering effect of linear probing.