Modified Search Problem: Directed Graph
- Recognize BFS/DFS can be carried on a directed graph.
- Trace the shortest path algorithm in an unweighted graph by specifying the values in auxiliary data structures.
- Analyze the running time of the (unweighted) shortest path algorithm, assuming an incidence/adjacency list Graph implementation.
The BFS/DFS algorithm can be carried out on a directed graph. The only adjustment would be to consider each vertex's "outgoing neighbors" during "exploration."
Consider the following directed graph:
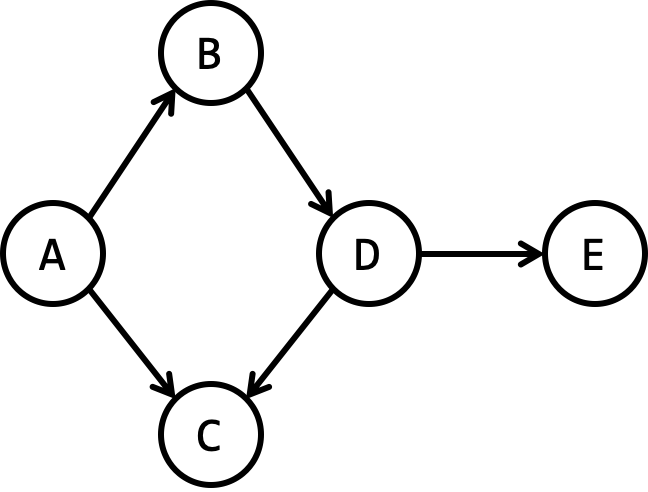
Exercise Carry out the BFS algorithm on the graph above starting at vertex $A$. Keep track of previous and distance values for each vertex. Reflect on the complexity of the algorithm.
Solution
- The algorithm's complexity is the same as the simple BFS algorithm; it runs in $\Omicron(N+M)$.
- The modified BFS requires more auxiliary space, although it is asymptotically linear (same as plain BFS).